I’ve brought up Simon Tatham’s Puzzle Collection here before. It was then, and still is now, one of the great wonders of the World Wide Web, a completely, utterly free, in both beer and libre, collection of randomly-generated puzzles of 40 different styles and counting, available for pretty much every platform. Not currently for Mac, because Simon’s Mac stopped working, but you’re free to compile it yourself if you can.
Let’s delineate the platforms: Windows, Linux, Mac (with the above caveat), Android, iOS, Java and even Javascript. You should be able to field one of those options, right? And which puzzles are provided? Black Box, Bridges, Cube, Dominosa, Fifteen, Filling, Flip, Flood, Galaxies, Guess (Mastermind without the trademarked name), Inertia, Keen, Light Up, Loopy, Magnets, Map, Mines(weeper), Mosaic, Net, Netslide, Palisade, Pattern (a.k.a. Nonograms, or Picross), Pearl, Pegs, Range, Rectangles, Same Game, Signpost, Singles, Sixteen, Slant, Solo (genericized Sokoban), Tents, Towers, Tracks, Twiddle, Undead, Unequal, Unruly and Untangle. Not only will the software generate an endless of stream of puzzles for you to solve, often with a user-selected difficulty, but some platforms will even print out books of these generated puzzles for you to solve, along with an answer key.
The puzzles I’ve boldfaced are what I call Nikoli-style puzzles. Nikoli is a popular Japanese puzzle magazine, the original home of Sudoku, and has a particular kind of logic puzzle that’s really satisfying to play. They usually have simple rules, but with profound implications, and with some thought you can deduce processes to help you solve them. Sudoku aficionados will immediately know what I’m talking about. The main subject of this post is about one of these Nikoli-style puzzles, Dominosa.
Nikoli specializes in human-created puzzles, and Simon Tatham’s Puzzle Collection creates its puzzles by computerized process. These kinds of puzzles really are better when set by hand. But that doesn’t mean the automatically-generated kind doesn’t have its place.
Also, Simon Tatham’s puzzles are completely free, don’t track you, and don’t have ads, making them a real rarity in this money-desperate age. If you need any proof that the app stores of Apple and Google are rigged against you, then consider that the Puzzles have been available on both their platforms for over a decade, but their discovery algorithms never seem to surface them. (Here’s some help in finding them: Google Play, Apple App Store.)
To give you idea of what kind of puzzles these are, and to get you on your way to solving one kind of them, here are my observations about Dominosa. The rest of this post is pretty long, so this is your chance to check out if you don’t want basic tips on how to solve it.
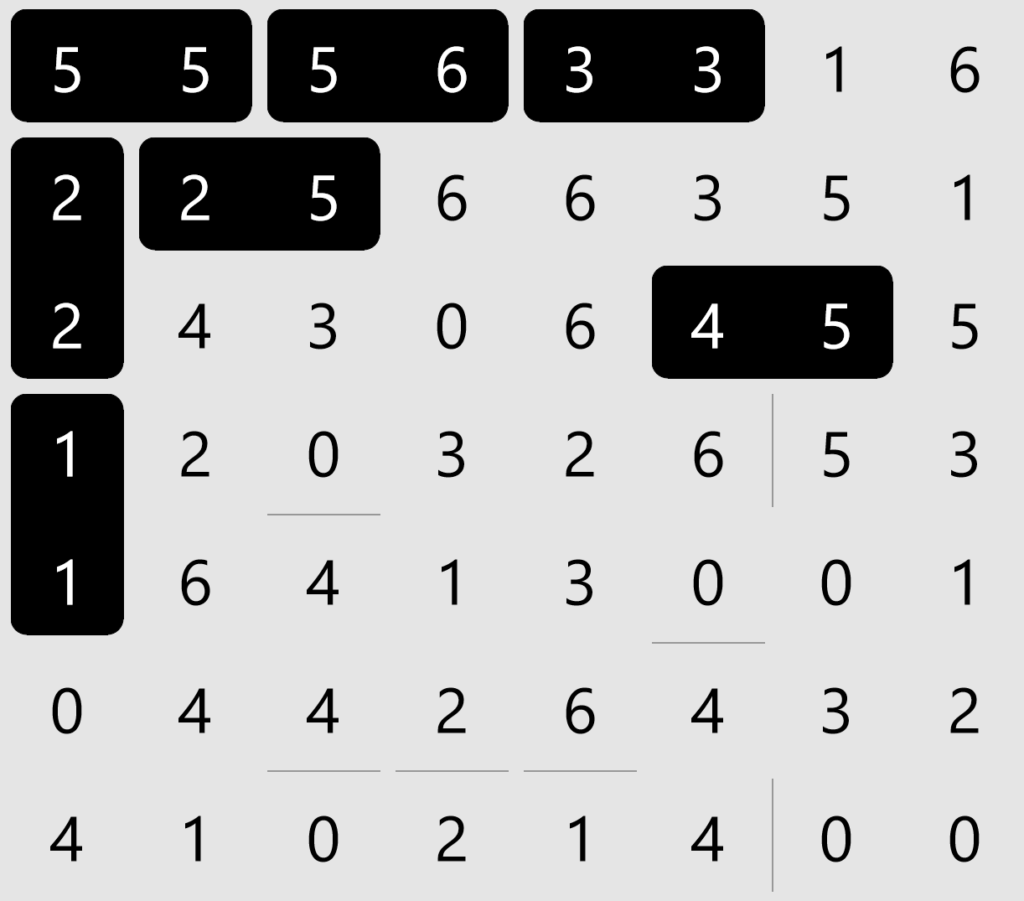
Dominosa presents you with a grid of numbers, usually from 0 to 6 (you can choose to solve larger puzzles). The numbers represent the values on a field of dominoes, but the edges between them have been removed, leaving only the numbers of pips that would be on their two sides. Your job is to place dominoes on the field, over the numbers, to reconstruct where they were originally. The puzzle is solved when every number is accounted for, filling the board with exactly one domino of each pair of values, with no contradictions.
I’ll present a series of images representing working out one of these puzzles at a basic level of difficulty. Not all of them are as simple as this.
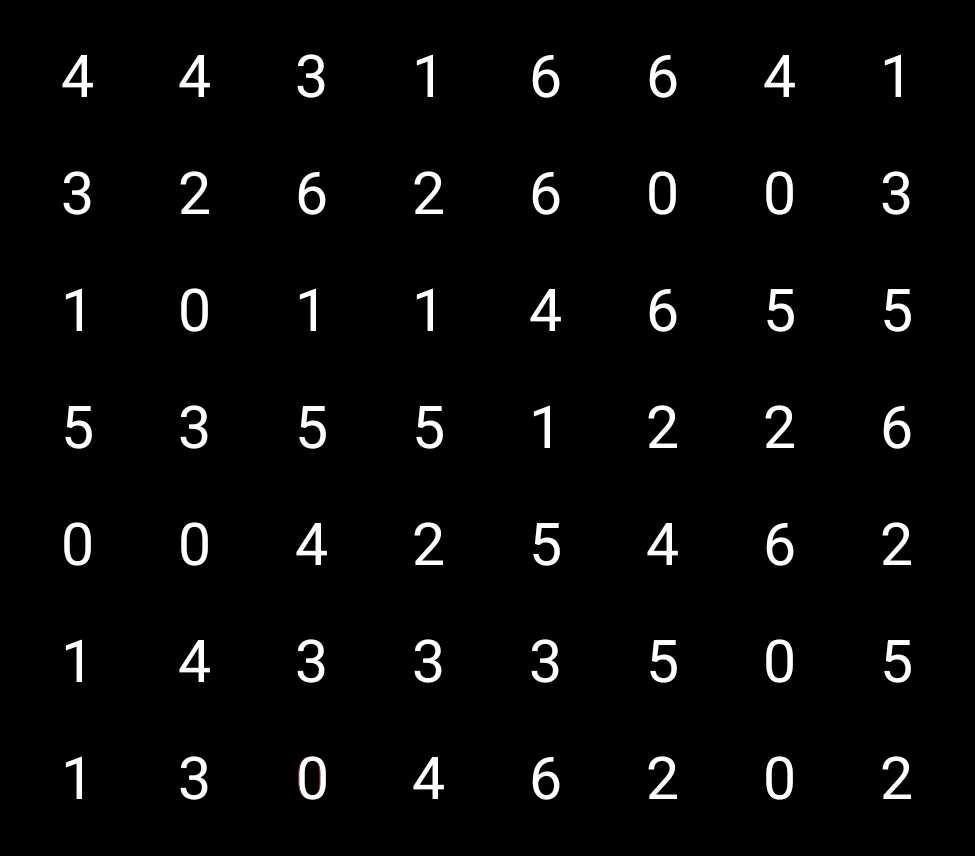
The way I solve these, I first look through for pairs of numbers. If you’re on a version of the Puzzles with keyboard support, you can press a number to highlight all of its values throughout the board. If you don’t have a keyboard, there will usually be number buttons onscreen that fill the same purpose. There may also be Undo/Redo buttons; if there aren’t, you can use Ctrl-Z/Ctrl-R for that.
I start out by looking for all the zeroes. Here they are:
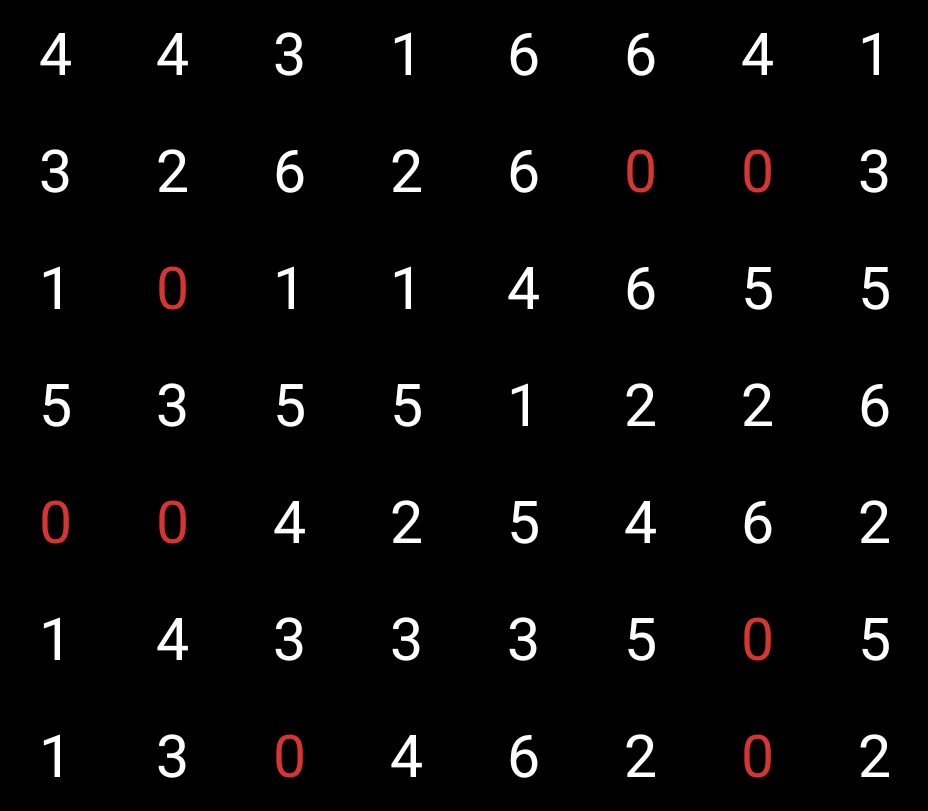
In a double-six puzzle like this one, there will always be eight of each digit. What I’m hoping to find is exactly one isolated pair of one of the numbers. There’s only one domino with each pair, from 0-0 through to 6-6, so a single pair means that a domino must be there.
No luck with Double-Zero, so I keep going, checking each number in turn. (You can only have up to two digits highlighted at once; pressing a number again turns off its highlighting.)
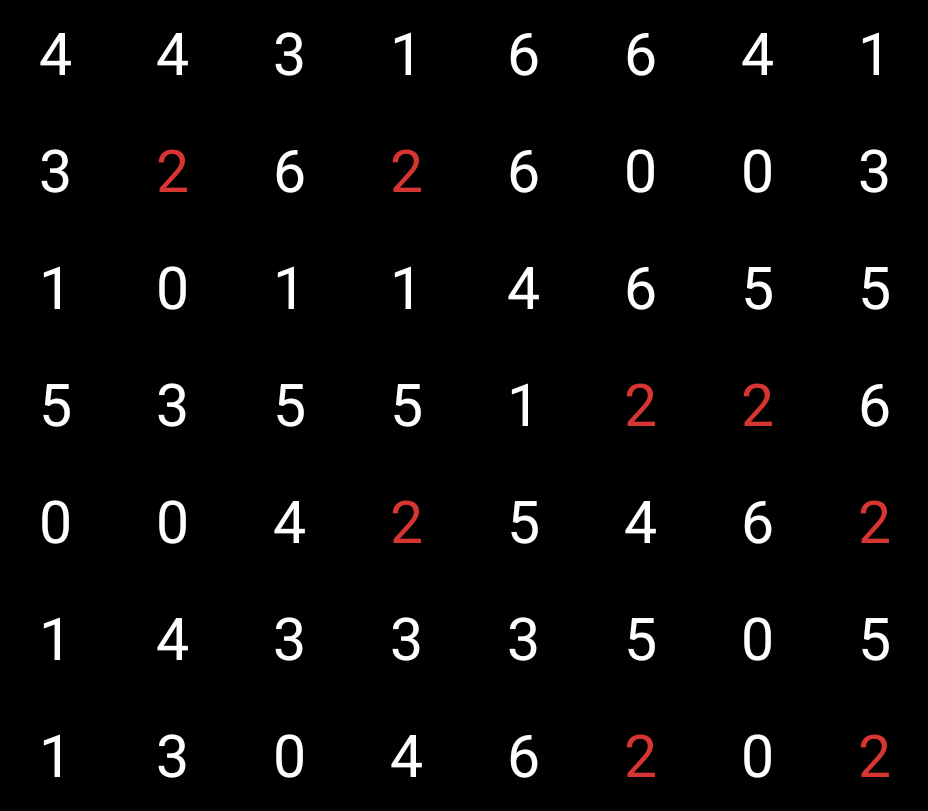
I have better luck with the 2s: there’s only one adjacent pair. So I click on the space between them to place a domino, as so:

In Nikoli-style puzzles, as you correctly fill out each little bit of the puzzle, it makes the rest of it slightly easier. When you make progress in solving it correctly, the puzzle seems almost to knit together, until the whole grid is complete.

It’s not just single pairs that are useful though. Sometimes you’ll find single triples, either in a straight line as here, or in an L-shape. So long as there aren’t any other adjacent digits of that value in the puzzle, then you know that one of the two possible pairs must be the correct one.
How is that useful? In the below case, there are borders between the digits that the two possible placements have in common. Since one or the other must be correct, the two domino edges that the possibilities share must be edges in the solution. We can mark edges in Dominosa with the right mouse button, or on mobile platforms with a long press:

Above I’ve placed the horizontal edges that the two possible Double-Three locations have in common.

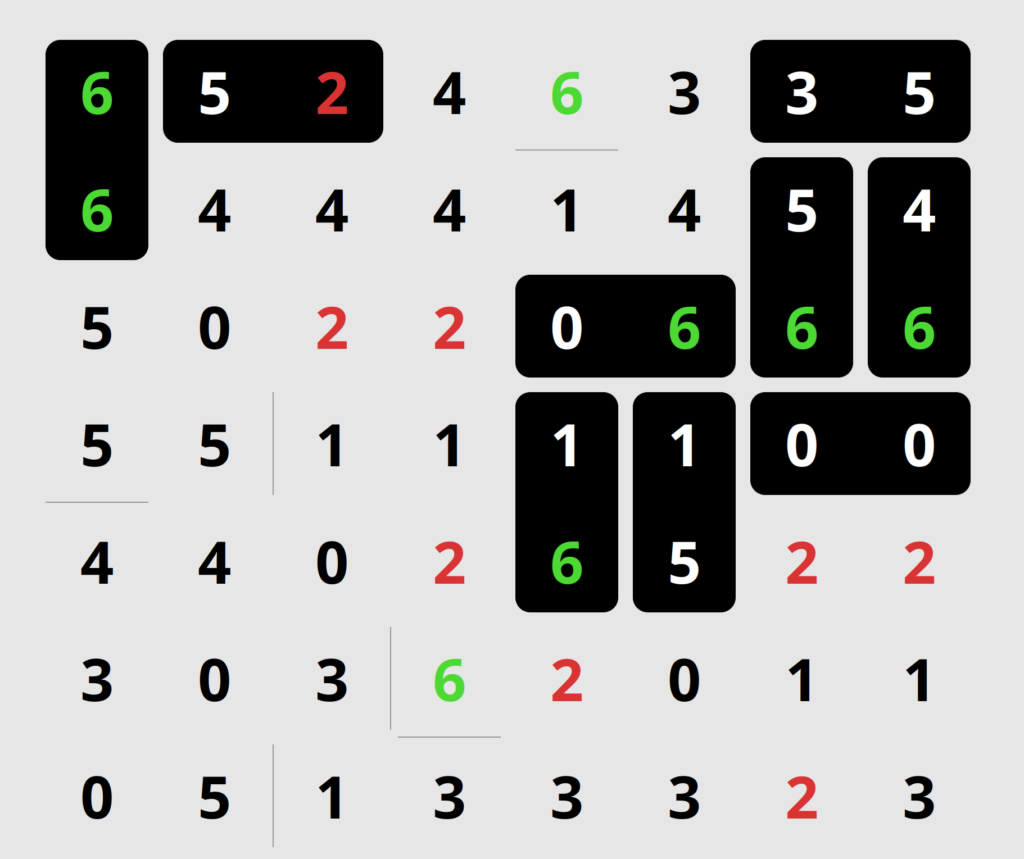
Moving on. There’s a single pair of 4s, so I’ve marked that domino. And there’s an L-shaped arrangement of three 6s. It’s on the outside of the puzzle, so there’s really just one edge to place, like so:

I’ve also started on the second step of the puzzle, looking for non-identical domino pairs. This is where the ability to highlight two different numbers becomes useful.
Now we’re looking for each possible 0-1 combo. There’s three possibilities here, which isn’t helpful.
The process I use is to check for the dominoes with one zero: 0-1, 0-2, 0-3, 0-4, 0-5 and 0-6. After that, the remaining pairs beginning with 1: 1-2, 1-3, 1-4, 1-5 and 1-6. When I move to the next digit, there’s fewer to check, because we’ve already done some: 2-3, 2-4, 2-5, 2-6; then 3-4, 3-5 and 3-6; then 4-5, 4-6, and finally 5-6.
Of the 1-2 domino, there’s only two places where it could be, so I can place edges alongside them. Also, there are two 1-6 pairs. But because we’ve ruled out one of them, when we tried the Double-Sixes, there’s only one pair left that could possibly be the domino.

Ah. Now we have one of the best things we can find: a dead-end. A place with a cul-de-sac, where a domino has to go regardless of its digits. Every digit in the puzzle must connect in one direction, and the 3 to the right of the 4-4 has only one way to go, so that must be where the 3-1 goes. And because of the two edges nearby, the 1-2 also has a location where it has to go.
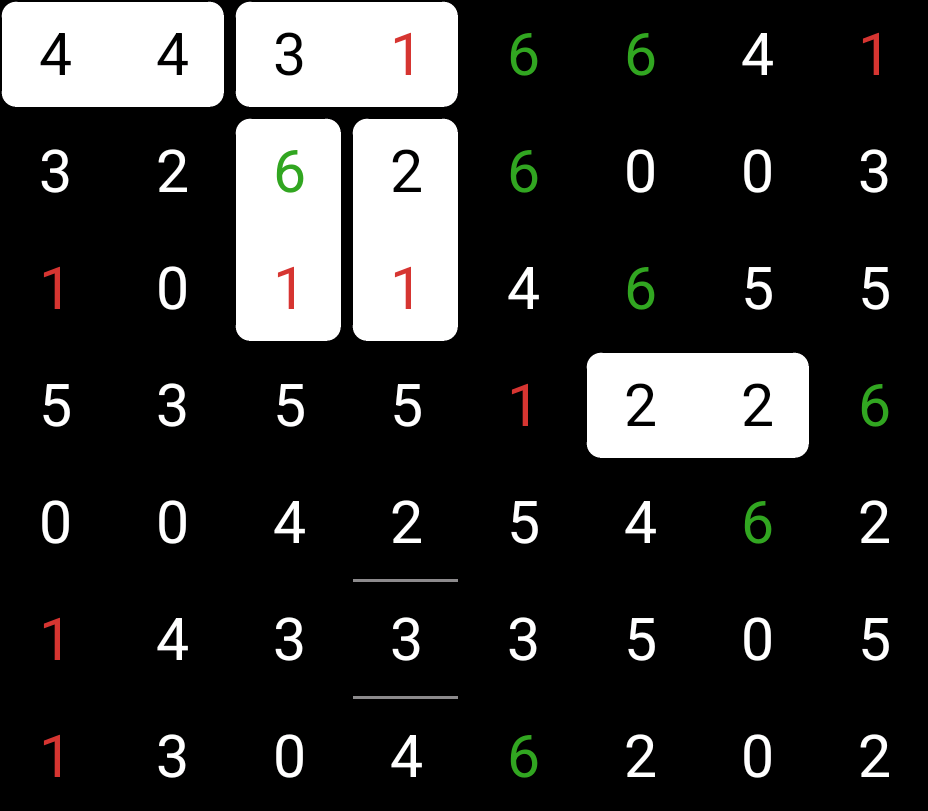
The great thing about these placements is, they weren’t narrowed down from the lack of other pairs of digits. Since the 3-1 has to go there regardless, all the other 1s by 3s on the board can’t be options, so we can place edges between those numbers.

We’re lucky again; each of these edges produces mandatory domino placements, in the same way!

These, in turn, allow us to place another domino, a 1-4, and to block an edge between another 1 & 4. It results in an unfilled region of the puzzle with only one entrance. Dominoes have exactly two ends, so any region containing an odd number of digits is impossible. This lets us place a useful edge, between a 5 and a 6, because if the edge were below the 6 instead, the region would have 11 digits in it.
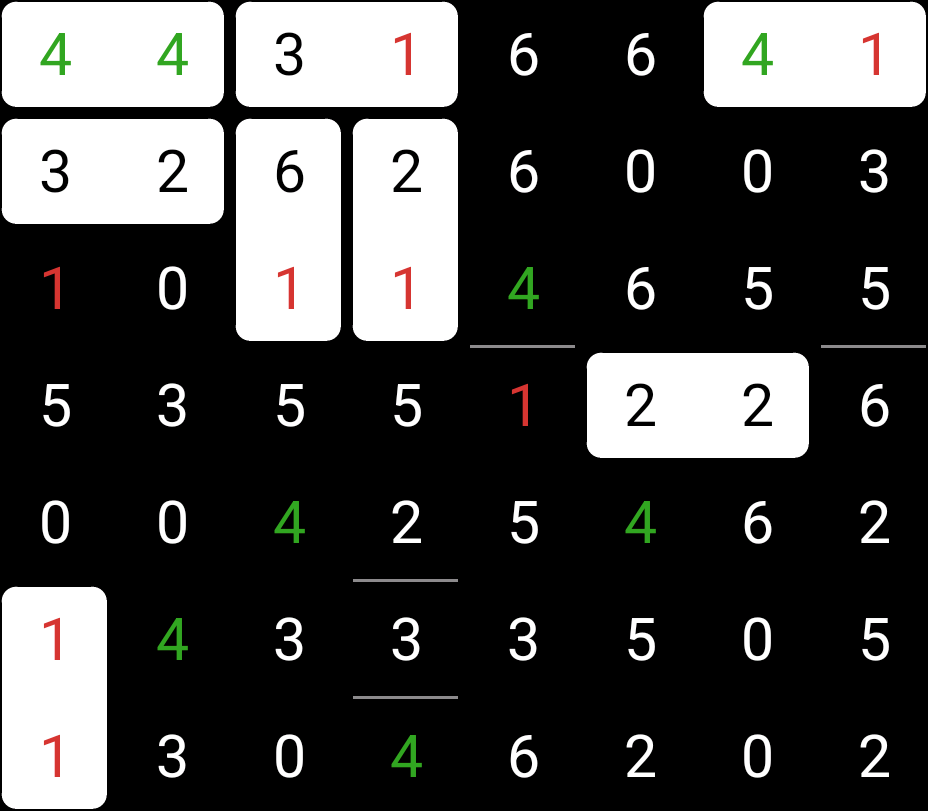
Continuing with checking for pairs, there’s a triple, a 1-5-1 with no alternatives around them. Since each puzzle must have exactly one 1-5, it has to be one of these two places, so all the other 1-5s in the puzzle must have edges between them.
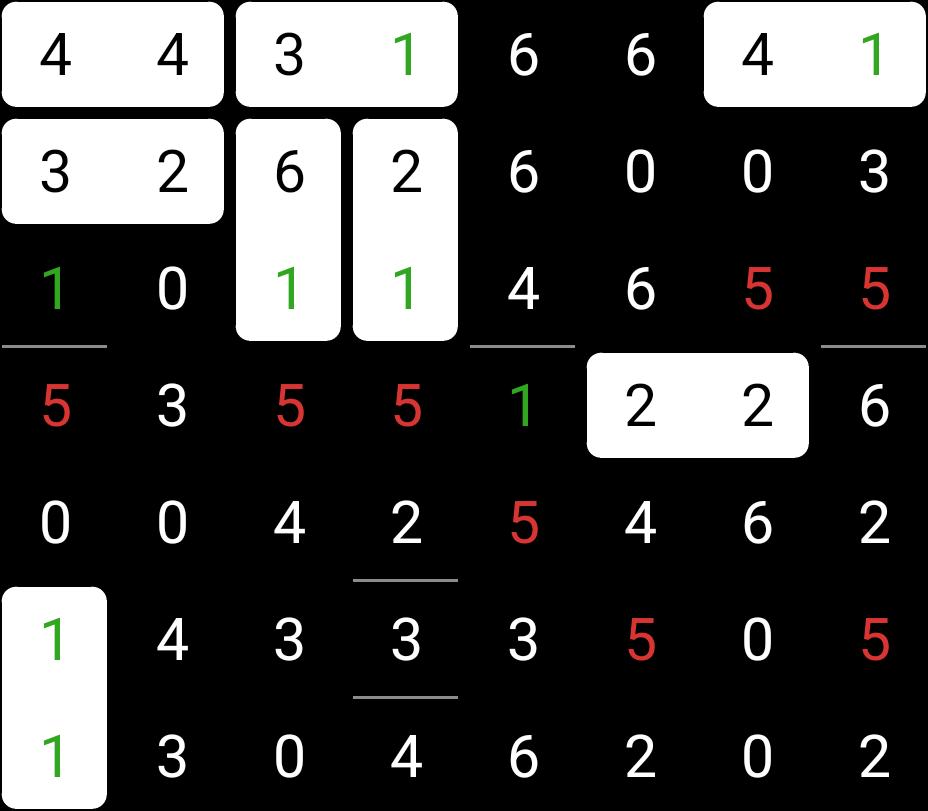
And that means a mandatory placement for the 1-0.
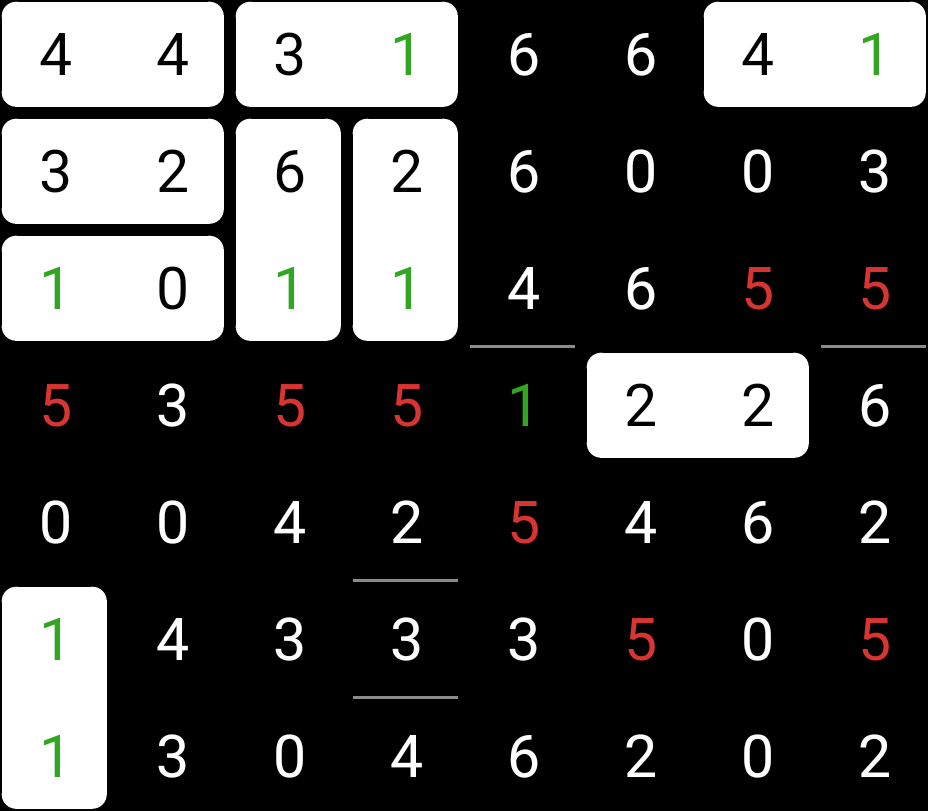
Hah, I neglected the mandatory 6-2 at the right side of the puzzle! But I did find a single remaining instance of a 2-4, which I filled in.
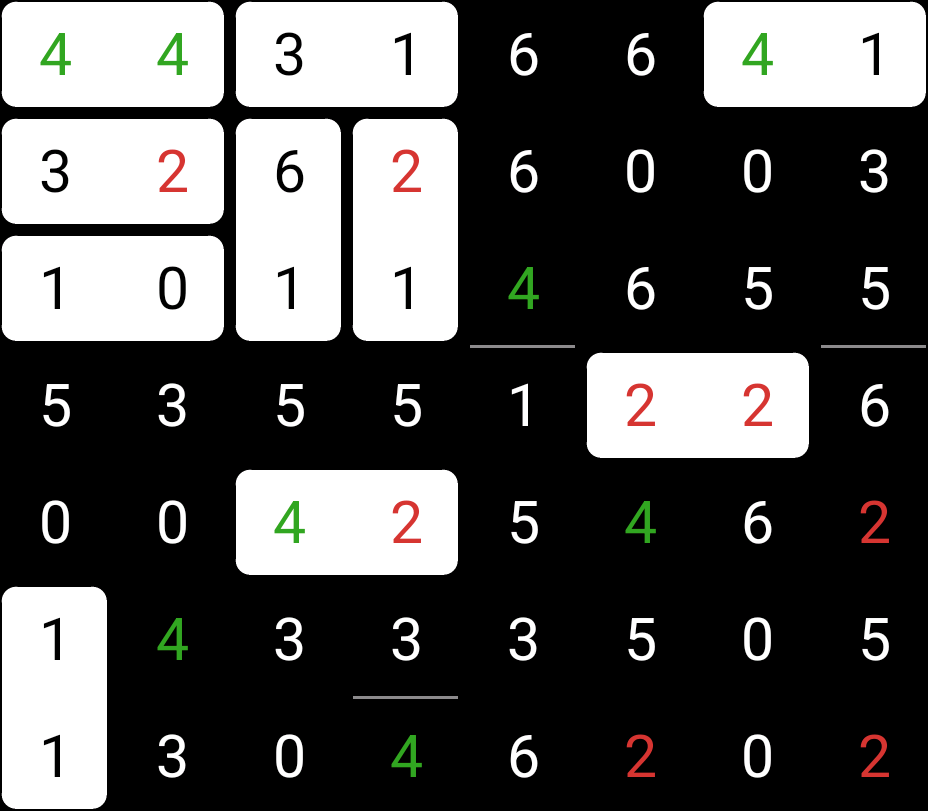
And then I noticed the 6-2:
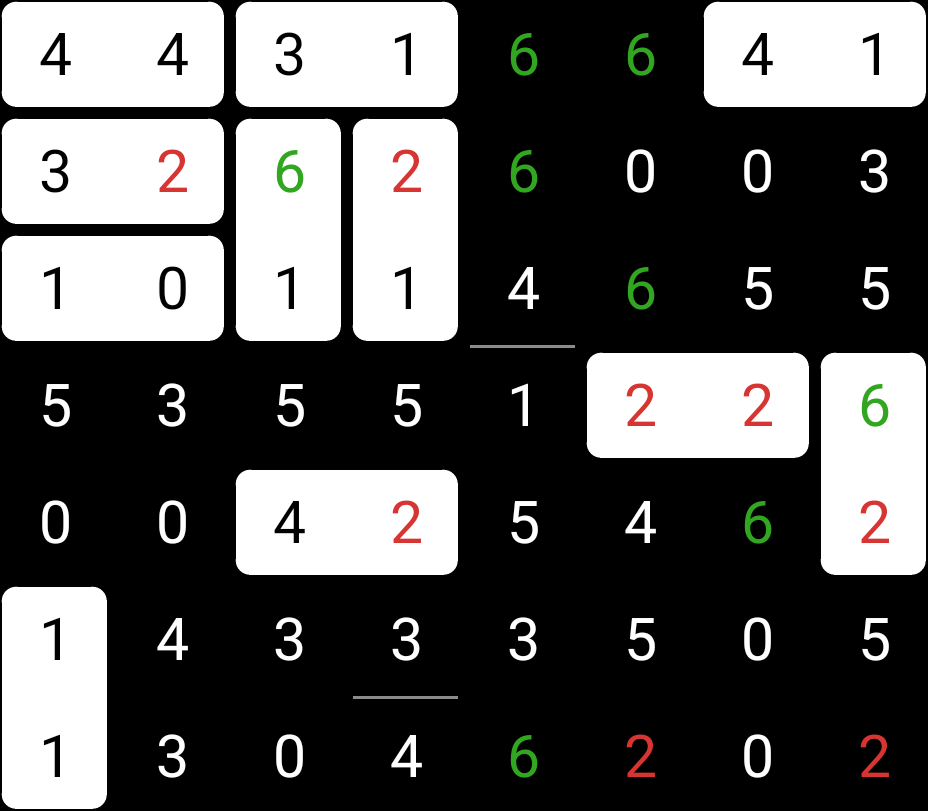
We’ve done about half the puzzle now, but really we don’t have much left to do. The 6-2 we place means we can place edges between the 2 and 6 at the bottom of the puzzle, as so:
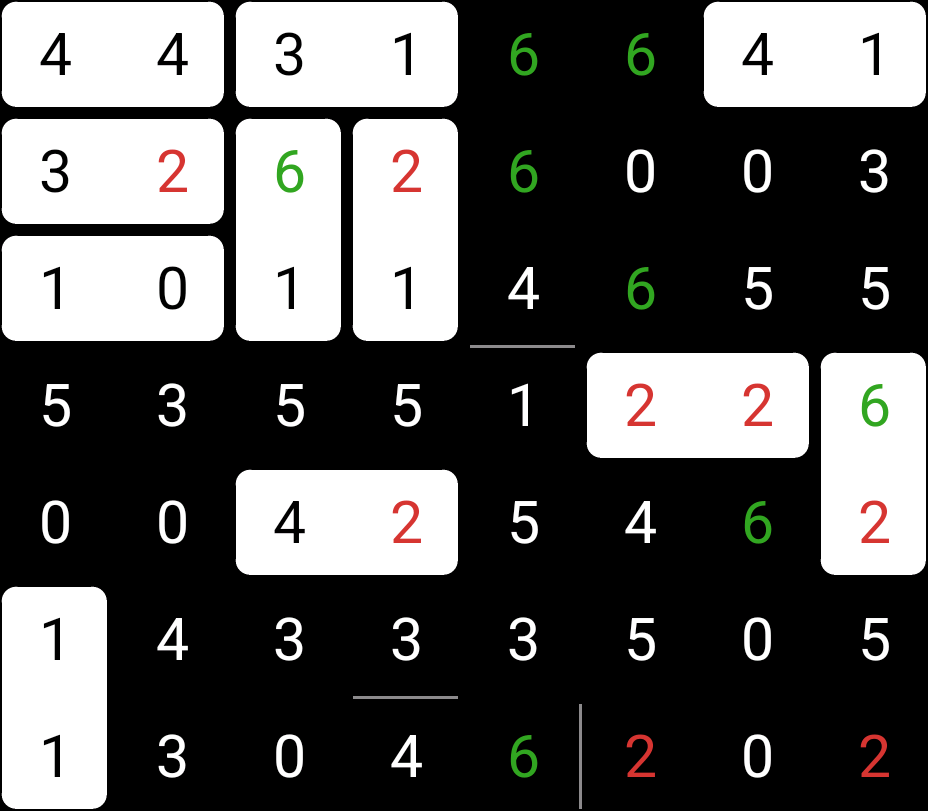
We can hurry through the rest of the puzzle. There’s a single triple of 3-4-3, so we can place an edge above its 4:
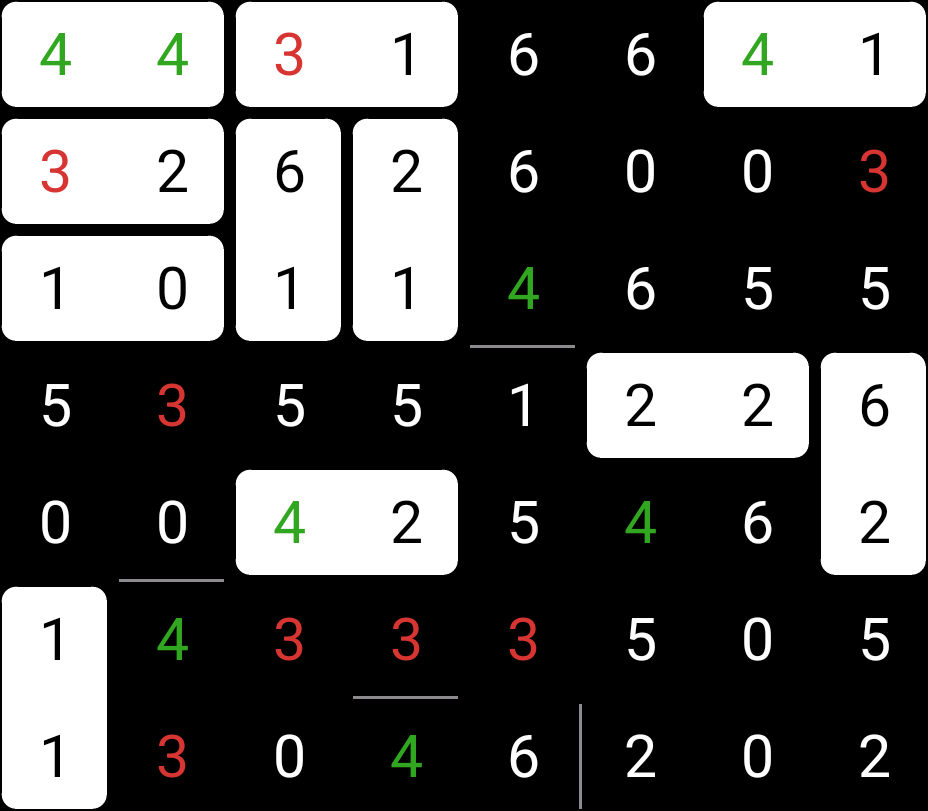
There’s a single 3-6:
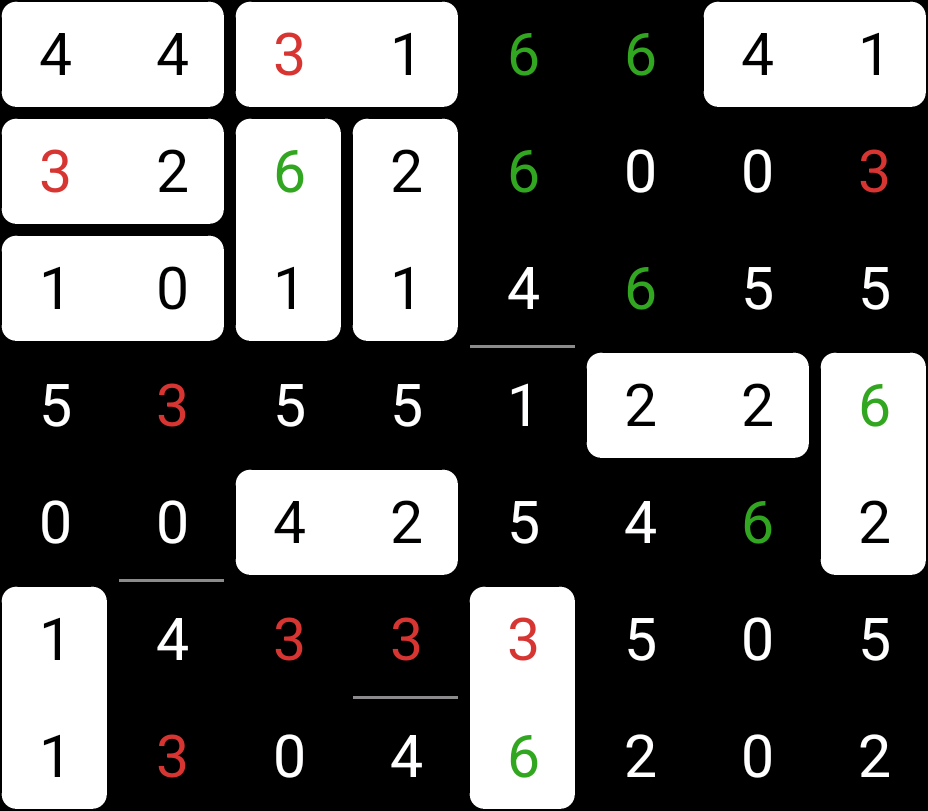
That creates two dead-ends, a Double-3 and 0-4, and then a 4-3:
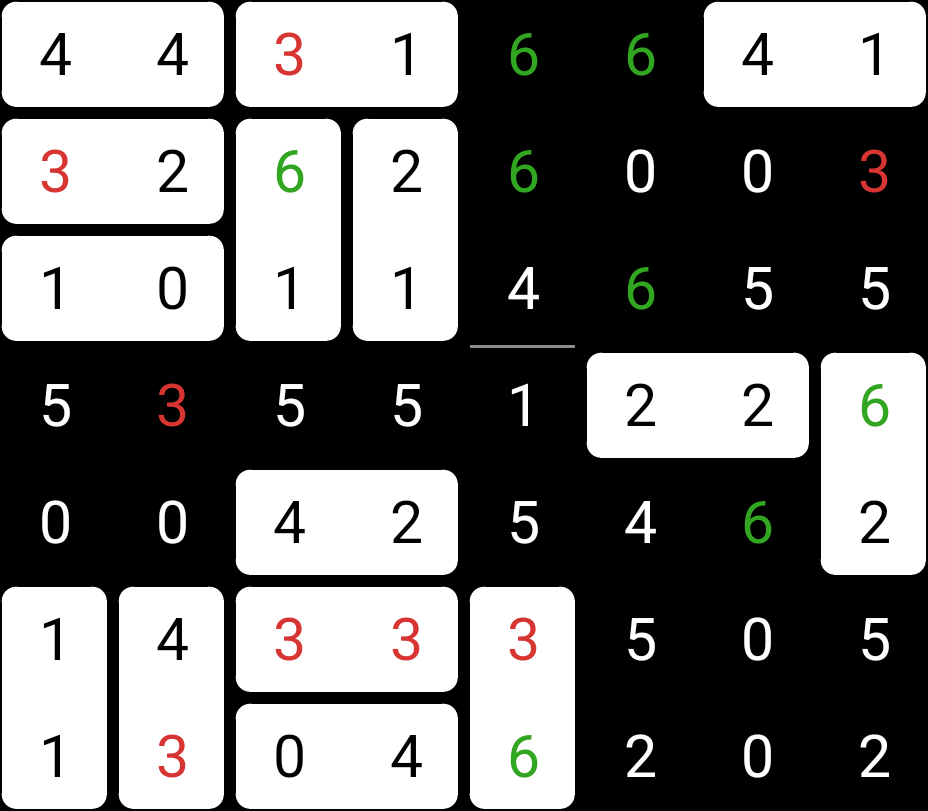
From here, most of the rest of it can be worked out with the same principles. When we get to small areas like this, often figuring out where to place one domino, or even edge, makes the rest of its region obvious. There’s a small region with a single path into it, so the fact that regions can only have an even number of digits comes into play again.
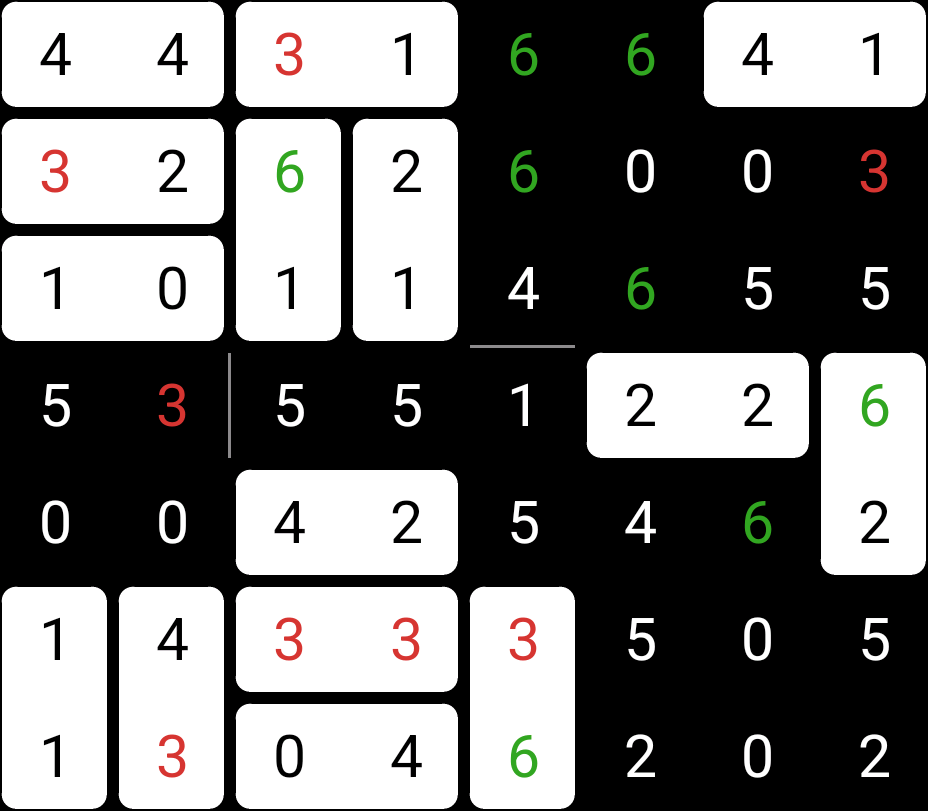
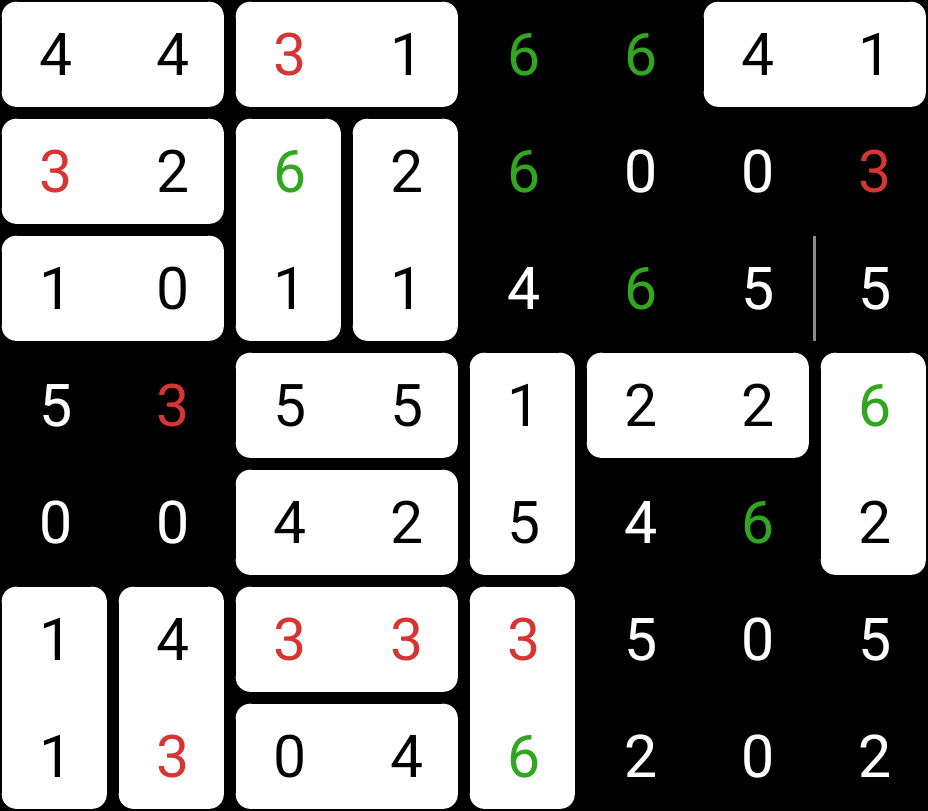
This puzzle is almost solved, so let’s just jump straight to the solution:
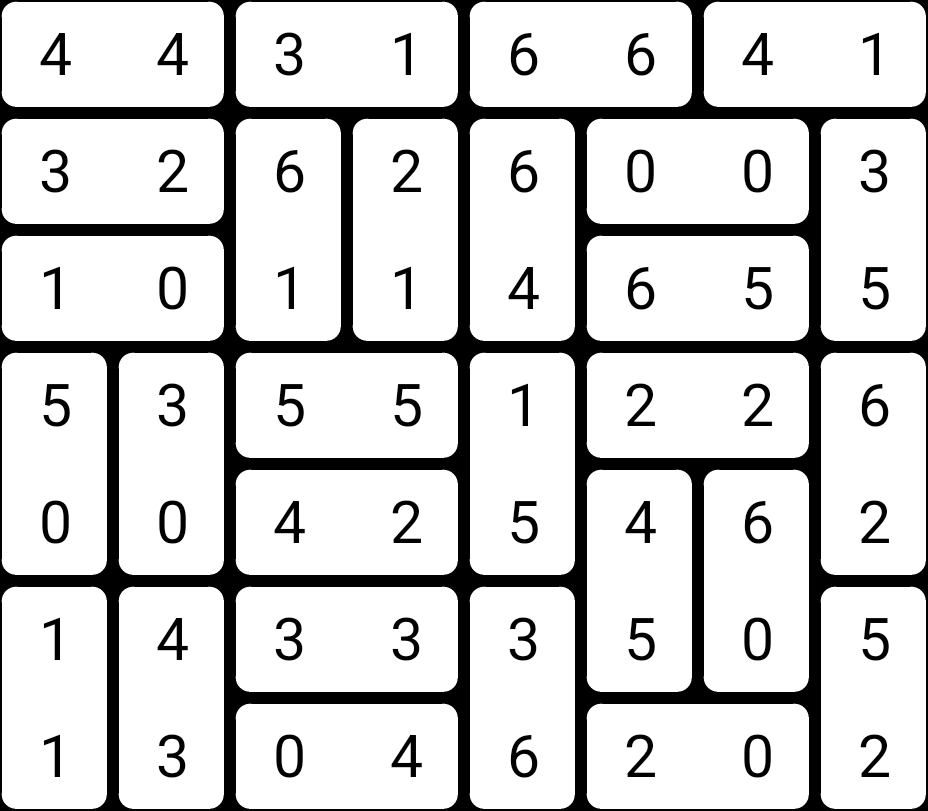
As noted before, most puzzles aren’t this easy. Often after you’ve been through all the possible pairs of digits, you still have a significant amount of puzzle left to do. Usually, if you look carefully at the puzzle, you can figure out placements that, if made, will result in contradictions to the rules of the puzzle. If you find one of those, you can then place an edge between its numbers.
There’s a couple more tricks I know of, but they start getting harder to explain easily here. I’m by no means an expert: I’m sure that experienced Dominosa solvers know tricks I have yet to figure out. I also don’t want to explain too much about how to solve these puzzles, as I got a lot of entertainment in figuring out my solving process, and I’d hate to deny that to you. Most of the processes I’ve mentioned so far are pretty obvious implications of the rules. Revealing the less obvious tricks feels a bit like a spoiler.
One great advantage you have in solving Nikoli-style puzzles on a computer is the Undo feature. Like doing Sudoku by hand, if you reach a point where tricks fail you and solving algorithms leave you stranded, you can progress by making assertions, basically guesses, then working them through until you reach a contradiction. There’s a whole strategy to this: you want to make a single binary, this-or-that guess, and to pick an unlikely guess, one that will prove itself incorrect quickly. Then you can erase the marks you made following your guess, and then mark its opposite.
On a computer, you can undo until the point where you made the guess, with Ctrl-Z. On paper, you’d not only have to remember all the marks you’d made since the guess, but you’d have to erase them all, which makes a huge mess. If you undo too far, you can press Ctrl-R to redo the removed moves. It’s really a tremendous aid!
Give Dominosa a try, and see what you can deduce. If you want to try some of the other Nikoli-style puzzles, that feel similar but have a different process, I recommend Loopy, Slant and Bridges.